作者:York_魚
发布时间:2018年3月15日
网络来源:简书
修订者:王建伯
修订时间:2020年1月4日
微博:比特币布道者
以下是对“赌徒破产”系列问题的研究总结。通过数学证明,可见“十赌九输”并非虚言。
PS:由于MarkDown不支持数学公式,所以下面问题的证明过程是通过 Daum Equation Editor来撰写,然后导出图片来展示。
庄家输掉所有筹码的概率
庄家有n个筹码,每次有概率p赢得一个筹码,或者概率q(q=1-p)输掉一个筹码。庄家输掉所有钱后,即终止游戏。假设各次赌博都是独立的,求庄家把所有筹码输光的概率。
解答如下:



推导过程修订,如下:


庄家输掉所有筹码的概率
这是上述数学公式的二维图形:
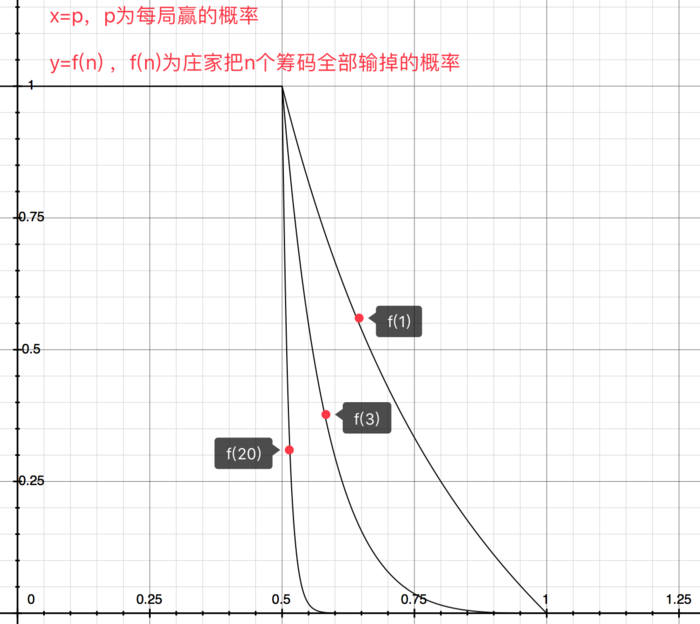

image.png
由公式和图可得:
- 当 p < q 时,庄家必然输光筹码
- 当 p >= q 时,p 相同时,庄家钱越多,输光筹码的概率越小
赌徒赢得N个筹码的概率
一个赌徒初始时有n个筹码,每次有概率p赢得一个筹码,或者概率q(q=1-p)输掉一个筹码。赌徒赢得N个筹码后,或者输掉所有钱后,即终止游戏。假设各次赌博都是独立的,求赌徒在输掉初始筹码前赢得N个筹码的概率。
解答如下:
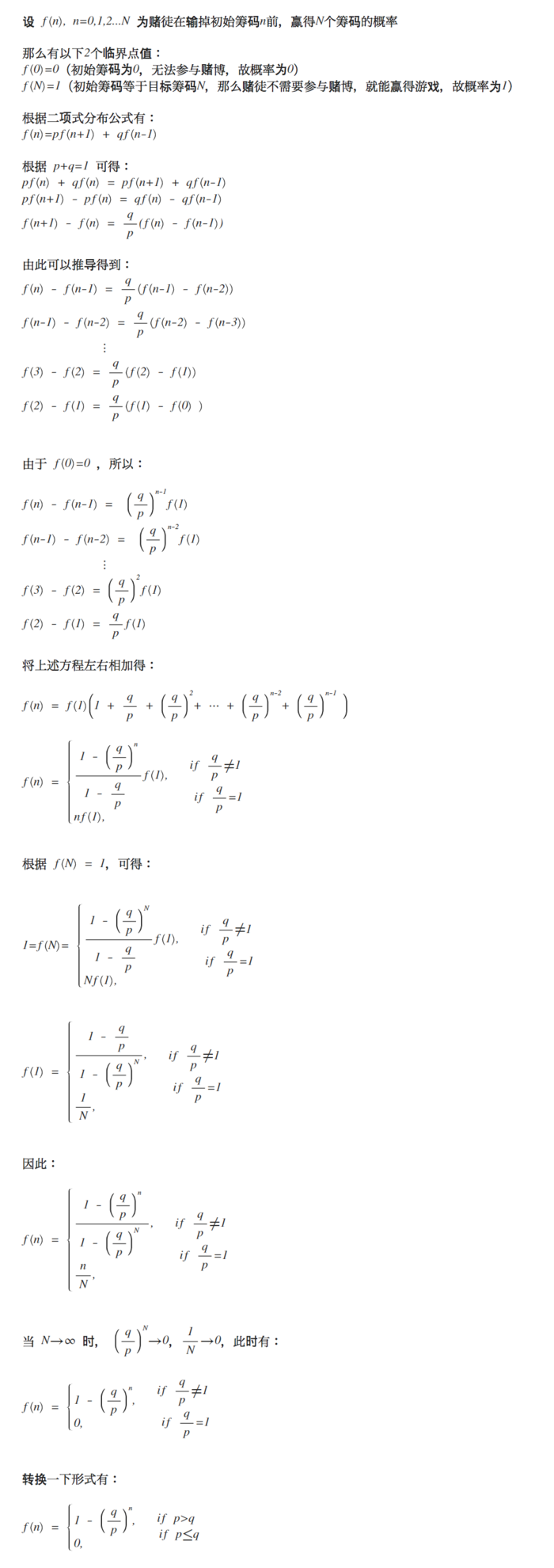

赌徒赢得N个筹码的概率
这是上述数学公式的二维图形:
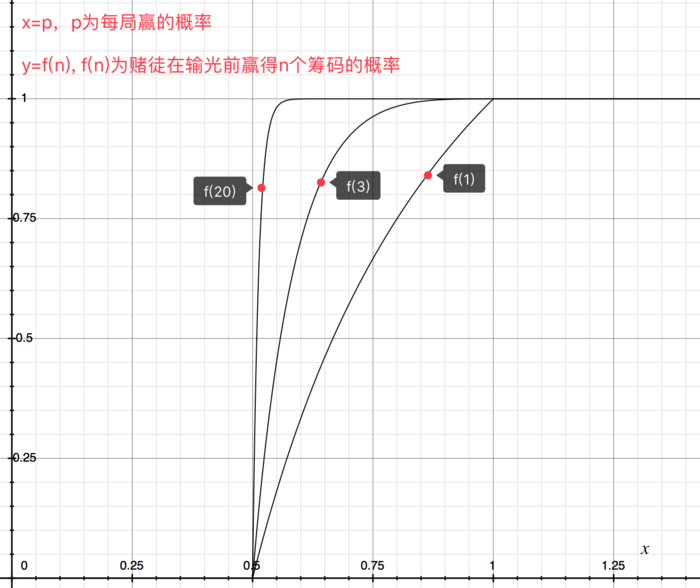

image.png
由公式和图可得:
- 当 p <= q 时,赌徒是无法赢得了目标筹码数目的
- 当 p > q 时,p 相同时,赢钱目标越大,赌徒赢取的概率越大
综合以上数学证明,再结合现实情况:
- 庄家的筹码往往多于一般赌徒
- 没有一个赌场会让赌徒赢的概率超过50%(即 p > q )
赌徒进去赌场后,在有钱的庄家面前,玩着不超过50%胜率的游戏,赢钱就只是一个美丽的泡沫。
如果你不想输钱,那就远离赌博吧——这是保证百分之一百不会输钱的方法。
作者:York_魚
链接:https://www.jianshu.com/p/7df33ae5fb56
來源:简书
简书著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。