发布时间:2019年12月30日
微博:比特币布道者
《比特币白皮书》二项分布、赌徒破产、泊松分布概率理解
1.二项分布
原文:
诚实链条和攻击者链条之间的竞赛,可以用二叉树随机漫步(Binomial Random Walk)(或称二项式随机行走)来描述。成功事件定义为诚实链条延长了一个区块,使其领先性+1,而失败事件则是攻击者的链条被延长了一个区块,使得差距-1。
理解:
二项分布:就是重复n次互相独立的随机试验,其特点是该随机试验只有两种可能结果:发生或者不发生、成功或者失败、要么0要么1、要么正面要么背面。
在攻击者追赶诚实链过程中,可以分割成无数“时间片”,在每个时间片内只有1次成功或1次失败两种可能,就如同扔硬币,每扔1次 (每个时间片)只有1次正面或1次背面,均符合二项分布。
2.赌徒破产
原文:
攻击者成功填补某一既定差距的可能性,可以近似地看做赌徒破产问题(Gambler’s Ruin problem)。假定一个赌徒拥有无限的透支信用,然后开始进行潜在次数为无穷的赌博,试图填补上自己的亏空。那么我们可以计算他填补上亏空的概率,也就是该攻击者赶上诚实链条。
p=诚实节点找到下一区块的概率
q=攻击者找到下一区块的概率
q_z=攻击者在落后z个区块时追上诚实链的概率
当p≤q时,q_z=1
当p>q时,q_z=(q/p)^z
假设p>q,随着攻击者需要追上区块数量的增加,追上的概率呈指数下降。由于攻击者的成功概率低,如果他在早期没有幸运的追上,随着他进一步落后,追上的机会越来越渺茫。
理解:
当p≤q时,即攻击者掌握了50%及以上算力时,不管开始攻击者落后多少个区块,经过无限次攻击,攻击者最终会追上诚实链,所以q_z=1。
当p>q时,攻击者落后z个区块时,攻击者需要连续追上z个区块来追上诚实链,攻击者连续追上z个块的概率q_z=(q/p)^z。三种理解:
1)根据赌徒破产问题,推导出概率公式,详见《Gambler’s Ruin Problem(赌徒破产问题)》
2)在无限长的时间内:
被切割成无数个时间片,在每个时间片内,攻击链成功的概率(攻击链追上1个区块的概率)是q/p,所以连续z个时间片成功的概率(攻击链追上z个区块的概率)是(q/p) ^z。
3)在无限长的时间内:
当落后1个区块时,追上的概率是二者分别爆1个区块的概率之比,即q/p。
当落后2个区块时,追上的概率是二者分别连爆2个区块的概率之比,即q^2/p^2=(q/p) ^2。
……
当落后z个区块时,追上的概率是二者分别连爆z个区块的概率之比,即q^z/p^z=(q/p) ^z。
3.泊松分布
3.1原文:
收款人将等待交易出现在首个区块中,然后在等到z个区块链接其后。此时,他仍然不能确切知道攻击者已经进展了多少个区块,但是假设诚实区块将耗费平均预期时间以产生一个区块,那么攻击者的潜在进展就是一个泊松分布,分布的期望值为:z*q/p。
理解:
攻击者的潜在进展:虽然诚实节点已经在交易后链接了z个区块,但是攻击者同步在生成伪链,伪链的长度为k,即攻击者的潜在进展为k,k的分布属于泊松分布,期望值lamda = z*q/p,其概率为:lamda^k*e^(-lamda)/k!。
泊松分布是由二项分布推导而来,是二项分布的近似值,是为了便于对二项分布进行计算。泊松分布的详解见《泊松分布的来源—公式推导—应用》。
期望值:在概率论或统计学中,期望值是指在一个离散性随机变量试验中“每次可能结果的概率乘以其结果”的总和,即试验的平均值。
链接了z个区块的情况下,对于潜在进展k个区块,每个进展的概率是q/p,所以期望值是z*q/p。
3.2原文:
当此情形,为了计算攻击者追赶上的概率,我们将攻击者取得进展区块数量的泊松分布的概率密度,乘以在该数量下攻击者依然能够追赶上的概率。
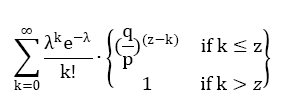
化为如下形式,避免对无限数列求和:
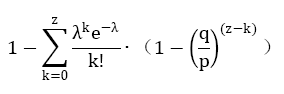
理解:
如果k大于z,说明攻击者潜在的进展k,已经超过了诚实链中交易后链接的z个区块,所以攻击者完胜,追上的概率为1。
如果k小于等于z,则由攻击者潜在进展情况概率lamda^k*e^(-lamda)/k!乘以该情况下的追上诚实链的概率(q/p)^(z-k)。
对于k小于等于z的情况,其由两个互相独立事件构成:
1)潜在进展k个区块事件,其概率是lamda^k*e^(-lamda)/k!。
2)从第k+1区块开始,追至第z个区块的事件,其概率是(q/p)^(z-k)。
最后的公式变换,将k的取值范围由0至无穷,变换成了0至z,避免了对无穷数列求和。1-(q/p)^(z-k)是“从第k+1区块开始,追不到第z个区块的概率” 。最后整体再用1去减,即又变成了追上的概率。