网络来源:深入浅出区块链
发布时间:2017年11月15日
非对称加密技术,在现在网络中,有非常广泛应用。加密技术更是数字货币的基础。
所谓非对称,就是指该算法需要一对密钥,使用其中一个(公钥)加密,则需要用另一个(私钥)才能解密。
但是对于其原理大部分同学应该都是一知半解,今天就来分析下经典的非对称加密算法 – RSA 算法。
通过本文的分析,可以更好的理解非对称加密原理,可以让我们更好的使用非对称加密技术。
题外话:
本博客一直有打算写一系列文章通俗的密码学,昨天给站点上 https, 因其中使用了 RSA 算法,就查了一下,发现现在网上介绍 RSA 算法的文章都写的太难理解了,反正也准备写密码学,就先写 RSA 算法吧,下面开始正文。
RSA 算法原理
RSA 算法的基于这样的数学事实:两个大质数相乘得到的大数难以被因式分解。
如:有很大质数 p 跟 q,很容易算出 N,使得 N = p * q,
但给出 N, 比较难找 p q(没有很好的方式, 只有不停的尝试)
这其实也是单向函数的概念
下面来看看数学演算过程:
- 选取两个大质数 p,q,计算 N = p q 及 φ (N) = φ (p) φ (q) = (p-1) * (q-1)
三个数学概念:
质数 (prime numbe):又称素数,为在大于 1 的自然数中,除了 1 和它本身以外不再有其他因数。
互质关系:如果两个正整数,除了 1 以外,没有其他公因子,我们就称这两个数是互质关系(coprime)。
φ(N):叫做欧拉函数,是指任意给定正整数 N,在小于等于 N 的正整数之中,有多少个与 N 构成互质关系。如果 n 是质数,则 φ(n)=n-1。
如果 n 可以分解成两个互质的整数之积, φ(n) = φ(p1p2) = φ(p1)φ(p2)。即积的欧拉函数等于各个因子的欧拉函数之积。 - 选择一个大于 1 小于 φ(N) 的数 e,使得 e 和 φ(N) 互质
e 其实是 1 和 φ(N) 之前的一个质数
- 计算 d,使得 de=1 mod φ(N) 等价于方程式 ed-1 = k φ(N) 求一组解。
d 称为 e 的模反元素,e 和 φ(N) 互质就肯定存在 d。
模反元素是指如果两个正整数 a 和 n 互质,那么一定可以找到整数 b,使得 ab 被 n 除的余数是 1,则 b 称为 a 的模反元素。
可根据欧拉定理证明模反元素存在,欧拉定理是指若 n,a 互质,则: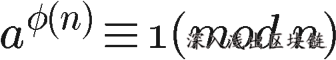
a^φ(n) ≡ 1 (mod n) 及 a^φ(n) = a * a^(φ(n) – 1), 可得 a 的 φ(n)-1 次方,就是 a 的模反元素。 - (N, e) 封装成公钥,(N, d) 封装成私钥。
假设 m 为明文,加密就是算出密文 c:
m^e mod N = c (明文 m 用公钥 e 加密并和随机数 N 取余得到密文 c)
解密则是:
c^d mod N = m (密文 c 用密钥解密并和随机数 N 取余得到明文 m)私钥解密这个是可以证明的,这里不展开了。
加解密步骤
具体还是来看看步骤,举个例子,假设 Alice 和 Bob 又要相互通信。
- Alice 随机取大质数 P1=53,P2=59,那 N=53*59=3127,φ(N)=3016
- 取一个 e=3,计算出 d=2011。
- 只将 N=3127,e=3 作为公钥传给 Bob(公钥公开)
- 假设 Bob 需要加密的明文 m=89,c = 89^3 mod 3127=1394,于是 Bob 传回 c=1394。 (公钥加密过程)
- Alice 使用 c^d mod N = 1394^2011 mod 3127,就能得到明文 m=89。 (私钥解密过程)
假如攻击者能截取到公钥 n=3127,e=3 及密文 c=1394,是仍然无法不通过 d 来进行密文解密的。
安全性分析
那么,有无可能在已知 n 和 e 的情况下,推导出 d?
- 模运算加减法:
(a + b) mod p = (a mod p + b mod p) mod p
(a – b) mod p = (a mod p – b mod p) mod p - 模运算乘法:
(a b) mod p = (a mod p b mod p) mod p - 模运算幂
a ^ b mod p = ((a mod p)^b) mod p
如果 n 可以被因数分解,d 就可以算出,因此 RSA 安全性建立在 N 的因式分解上。大整数的因数分解,是一件非常困难的事情。
只要密钥长度足够长,用 RSA 加密的信息实际上是不能被解破的。
补充模运算规则
- 模运算加减法:
(a + b) mod p = (a mod p + b mod p) mod p
(a – b) mod p = (a mod p – b mod p) mod p - 模运算乘法:
(a b) mod p = (a mod p b mod p) mod p - 模运算幂
a ^ b mod p = ((a mod p)^b) mod p
深入浅出区块链星球为各位解答区块链技术问题,欢迎加入讨论。
深入浅出区块链 – 打造高质量区块链技术博客,学区块链都来这里,关注知乎、微博 掌握区块链技术动态。