作者:氯化钡和硫酸银
时间:2014年2月4日 22:34
来源:http://blog.sina.cn/dpool/blog/s/blog_a661ecd50101axgy.html
欧拉函数有很多好玩的性质,这里补充一下…下次再说原根的事。
设 m为任意正整数,则欧拉函数 φ(m) 定义为 {1,2,3,…,m} 中与 m互素的整数的个数。不妨先观察一下一些比较小的数的欧拉函数:
φ( 1)= 1 φ( 2)= 1 φ( 3)= 2 φ( 4)= 2 φ( 5)= 4
φ( 6)= 2 φ( 7)= 6 φ( 8)= 4 φ( 9)= 6 φ(10)= 4
φ(11)=10 φ(12)= 4 φ(13)=12 φ(14)= 6 φ(15)= 8
φ(16)= 8 φ(17)=16 φ(18)= 6 φ(19)=18 φ(20)= 8
……
当然一般性的规律很难找,不过还是能看出一些特性的,比如下面这个:
1.若 m>=3 为整数,则 φ(m) 为偶数。
证明当然很容易,只需注意到两个和为 m 的数要么都与 m 互素,要么都不与 m 互素(事实上这两个数分别与 m的最大公约数是相同的)。这样, {1,2,3,…,m} 中的绝大多数都可以配对,剩下的只有 m ,如果 m 是偶数则还剩下m/2 ,而当 m>=3 时这两个数都不会与 m 互素。
2.若 p 为素数,则 φ(p)=p-1 。
这个容易理解,因为1,2,3,4,…,p-1 都与 p 互素。
3.若 p 为素数, k 为正整数,则 φ(p^k)=p^k-p^(k-1) 。
这个也不难。因为某个整数与 p^k 互素的充要条件是这个整数不能被 p 整除。从总数 p^k 中减去被 p 整除的数p^(k-1) 就是 φ(p^k) 的值。
下面的这个性质就比较牛B了:
4.若 a,b 是互素的正整数,则 φ(ab)=φ(a)*φ(b) 。
也就是说,两个互素的正整数相乘再求欧拉函数,等于两个数先求欧拉函数再相乘。证明用到了计数的方法:我们用两种方法数一下1,2,3,…,ab中与 ab 互素的整数的个数。
首先用定义立即得到这个数为 φ(ab) 。
然后,注意到一个整数与 ab 互素,当且仅当它与 a,b 均互素。
由前者推出后者:若一个整数与 ab 互素,它当然与 a,b 都找不出大于 1 的公因子。
由后者推出前者:若一个整数与 a,b 均互素,则这个整数拥有的素因子 a,b 都没有,把 a,b乘起来也凑不出这些素因子中的任意一个。
当然,这些用裴蜀定理也容易推出来。
这样,这个整数除以a 的余数有 φ(a) 种情况,除以 b 的余数有 φ(b) 种情况。又由中国剩余定理,这个整数除以 a,b的两个余数唯一确定了这个整数除以 ab 的余数(当然,如果这个整数在1,2,3,…,ab 的范围内,则这个整数显然也是唯一确定的)。再根据乘法原理,这个整数就可以取 φ(a)φ(b)个不同的值。
至此即证明了φ(ab)=φ(a)*φ(b) 是成立的。
接下来,我们的工具已经凑齐了,我们来推导任意正整数的欧拉函数计算公式:
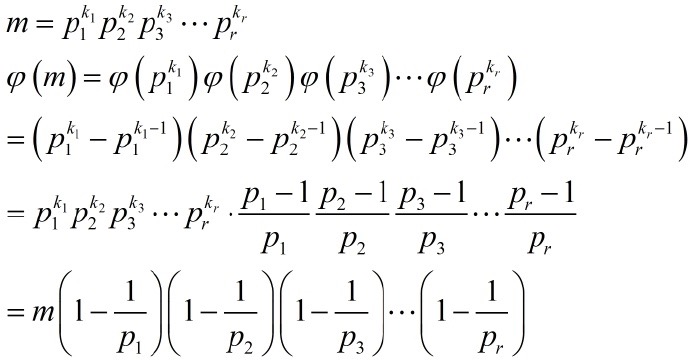
第一步把 m进行分解,分解后的各个底数是互不相等的素数,各个指数是正整数;后面的计算则利用了上面的第三、四条性质。图中第三行已经可以作为公式,但是我们习惯上也用最后一行进行运算。
最后再来看一个很好玩的结论:对于任意正整数 n ,则它的所有正因子(所有约数)的欧拉函数求和恰好等于 n 。
写成公式就是
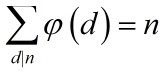
看起来很神奇,这个结论还有一个很简单的证法:
任取 n的一个正因子 d ,考虑在1,2,3,…, d 中与 d 互素的整数组成的集合。这个集合显然有 φ(d) 个数。现在让这个集合的每个数都乘以n/d (这当然也是个整数),则这个集合恰好是所有 1,2,3,…,n 中与 n 的最大公约数为 n/d的数构成的集合(不妨记作 A(d) ),它也含有 φ(d) 个数(这是因为两个数分别除以二者的最大公约数后,商互质)。
一个整数大于等于 1 小于等于 d ,等价于这个整数乘以 n/d 之后大于等于 1 小于等于 n。这个是显然没问题的。
一个整数与 d 互素即 (x,d)=1 ,等价于 x 乘以 n/d 之后与 d乘以n/d后(即n)的最大公约数为 n/d ,即(x*(n/d),d*(n/d))=1*n/d,这显然就是求最大公约数的两个数同时扩大某个倍数,二者的最大公约数当然也会扩大同样的倍数。
后面就快了,考虑n 的所有正因子 d ,那么由上述操作得到的所有 A(d) 显然两两交集为空,并集为 1 到 n 的所有整数(因为它们与 n的最大公约数肯定是 n 的约数,而 n/d 恰好可以取到 n 的所有约数)。我们立即得到所有 φ(d) 的和为 n 。
另外当然可以去直接计算。我们把 n 和它的任意一个正因子 d 分解素因数:
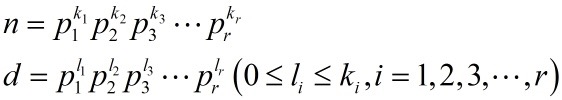
这样的话,利用欧拉函数的性质就可以进行如下变形:
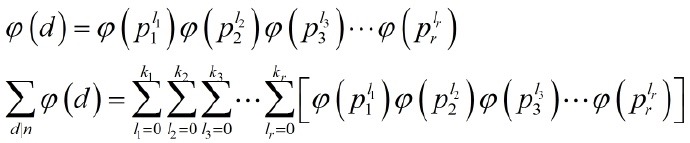
注意左边的 r个求和号恰好表示 0<=l_i<=k_i 的意思。利用乘法分配律,这个式子显然是成立的:
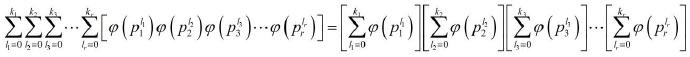
右边每个中括号里的式子都好求,把求和的式子拆开来写,会发现可以一项一项消掉,最后每个中括号恰好等于 p_i 的 k_i次方。这就证明了这个式子等于 n 。