作者：氯化钡和硫酸银
时间：2014年2月5日 22:48
来源：http://blog.sina.cn/dpool/blog/s/blog_a661ecd50101axpi.html
指数的概念，其实小学的时候就有点沾边了…比如像下列这种探究规律的题目：
3^1,3^2,3^3,3^4,… 的个位数字有什么规律？
也就是说 3^x除以 10 的余数有没有什么规律，结果当然是 3,9,7,1 循环…把底数 3换成别的数，结果还是循环。当然，现在应该可以看出点更深入的东西了：
1.只要有重复，必然有循环。每个位置上的余数都是由前一个余数唯一确定的（乘以底数，再取余数：(3^k*3)mod 10=(3^k mod 10 * 10) mod 10），所以如果有两个余数相等了，那么把它们都往后推一项，余数还是相等的，再往后推一项余数仍相等，依次类推。结果就是从某一项开始，所有“距离”一定的两项余数都相等（还记得周期函数定义f(x+T)=f(x) 吧）。这样就有了周期性。
2.重复总会出现。这是显然的，因为余数的情况只有有限个，而数列却有无限项。余数不可能不重复。
实际上，如果我们限定底数与模必须互质（比如 3 和 10 ），那么还有一个性质：
3.从第一项就开始循环。因为这回多了个条件：每个位置上的余数可以由后一个余数唯一确定。
假如这个位置上的余数不确定，有两个不同的值，那么由此算出来后一个余数的两个值也不一样（这是由底数与模互质推来的，还记得费马小定理怎么证的吧）。
所以如果有两个余数相等了，那么我们往前推就可以推到第一项与某一项相等。所以循环从第一项就开始了。
另外，假如我们把底数的 0 次方作为第一项，并没有影响上面的论证。这样第一项保证是 1 。既然这样，后面究竟到什么时候第二次出现 1就成了一个很关键的问题。比如说，这一项的指数就等于循环节的长度。
我们给它一个定义：
设 a,m 为互素整数且 m>=2 ，则使 a^r≡1(mod m) 成立的最小正整数 r 记为 a 模 m的指数，符号为
（指数还有某些其它的名称，比如说“次数”，“阶”…
另外好像这个记号很不统一…《数论概论》上用 e 代替了 ord ，并且在 a 外面加括号…
如果没有用 Mathtype ，则上面的指数符号记为 ord_m(a) 。
另外上面斜体字里边有个同余号变成两横了，就是下面一横比较粗那个…别看成等号了）
接下来研究一下a^x mod m 的循环到底是怎么回事。先证明这个结论：
设 a,m 为互素整数且 m>=2 ，则非负整数 x 满足 a^x≡1(modm) 的充要条件是 x 是 ord_m(a) 的倍数。
证明比较简单。
如果 x 是 ord_m(a) 的 k 倍，那么 a^x 除以 m 的余数显然是 1 ，因为 a^x 同余于 1 的 k次方。
反过来，如果 a^x 除以 m 的余数是 1 ，那么设 x 除以 ord_m(a) 的商是 k ，余数是 r，则左边可以通过分离出 a^ord_m(a) （这就相当于 1 ）的 k 次方而剩下 a^r ，其中r 小于 ord_m(a) ，又由指数定义中的“最小”两字得知 r 只能等于 0 。所以 x 是 ord_m(a)的倍数。
由此可由欧拉定理立即得推论： φ(m) 是 ord_m(a) 的倍数。
接下来又是一个类似结论：
设 a,m 为互素整数且 m>=2 ，则非负整数 x,y满足 a^x≡a^y(mod m) 的充要条件是 x,y 模ord_m(a) 同余。
这个也可以视为一个推论，不妨设 x>=y ，则两边约去 a^y （因为 a^y,m互素），立即转化为上面的那个结论（只不过指数换成了 x-y ）。
这样就搞清楚了，数列 a^x mod m （前提条件是 m>=2 且 (a,m)=1 ）的循环节为 ord_m(a)，每个循环节内没有两项相同，并且第一项为 1 。
另外，关于指数还有一些比较“高级”的性质：
1.设 m>=2 为整数， x,y为正整数，则有
中间那个符号表示左边可以推出右边，但是反过来不一定成立。
我们用指数的定义来证明它：
首先，由于 xy 是 a 模 m 的指数，显然有 (a^x)^y=a^(xy) 被 m 除的余数为 1。
其次，如果 (a^x)^y≡1(mod m) 中的 y 可以换成更小的正整数 y’ ，那么就有a^(xy’)≡1(mod m) ，这样 xy 就不是 a 模 m 的指数了。
这个结论的逆命题是错的，反例很容易找，例如 ord_10(3^3)=4 ，但是 ord_10(3)=4 而不是 12。
2.设 m>=2 为整数，则有
证明如下：
首先，由于 a^x,b^y 模 m 都余 1 ，容易得到 (ab)^xy=(a^x)^y*(b^y)^x 模 m余 1。
其次，若 ab 的 k 次方模 m 余 1 ，则有 1≡(ab)^(xk)≡b^(xk)(mod m) ，于是 xk应该是 b 模 m 的指数的倍数即 y 的倍数，又 x,y互质，则 k 必为 y 的倍数。同理 k 是 x 的倍数，所以正整数 k 最小值为 xy。
这些性质后面都会用到。
前面说过，指数的定义中要求 a,m 互素。这样立即得到一个结论：因为 a^x 与 m 互素，所以 a^x 除以 m 的余数也与 m互素，这样这个余数只可能有 φ(m) 种不同的取值。
有的时候这些取值都能取到，比如说 a,m 分别为 3,10 的情况，我们发现余数可以取到 1,3,7,9 ，满足条件。如果底数换成 9，就不满足条件了，因为余数只能取到 1,9 。
注意到余数出现的不同值的个数恰好等于循环节的长度（因为每个循环节里的余数两两不等），于是余数可以取到所有φ(m) 个值就等价于 ord_m(a)=φ(m) 。
如果m>=2 是整数，我们把满足 ord_m(a)=φ(m) 的整数 a 叫做模 m的一个原根。关于原根有一个显然的性质，就是若x=0,1,2,3,…,φ(m)-1，则 a^x 恰好构成模 m 的一个“缩系”（即这 φ(m)个数都和 m 互素，并且模 m 两两不同余）。
这个性质太好了，如果我想算一下两个数乘积模 m 的值（这两个数都与 m 互素），那么只要 m 有一个原根 g ，就可以把这两个数与 g的多少次方同余找出来，再把两个次数加起来就行了。
如果 m,g均给定，那么对任意与 m 互素的整数 a ，必然存在 0,1,2,3,…,φ(m)-1 中的唯一一个数 k 使得g^k≡a(mod m) ，这个数 k 叫做 a 的指标，记为 I(a) 。
容易证明下面的两个性质：
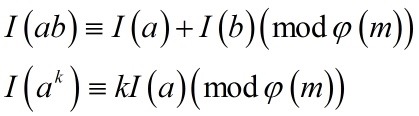
证明不说了。注意指标运算总是模 φ(m) 而不是模 m。由此指标也被称为离散对数。过去数论计算经常用指标表进行运算，现在离散对数还在密码学中扮演重要的角色。
接下来我们讨论一个很重要的问题：哪些数 m 是存在原根 g 的？确实有的数没有原根，比如 8 就没有原根（因为 φ(8)=4，但是任意与 8 互质的整数都是奇数，奇数的 2 次方除以 8 必然余 1，指数一定是 2 的约数，不可能是 4 ）。在2,3,4,5,…,30 这 29 个整数中，我们发现2,3,4,5,6,7,9,10,11,13,14,17,18,19,22,23,25,26,27,29
存在原根。把每个数都分解素因子，会发现存在原根的数除了 2,4之外，所有奇数均只含有一个素因子（或者说，它们都是某个奇素数的某个正整数次幂，包括 1次幂），所有偶数也是只含有一个奇素因子。
下面我们就一步一步证明：整数 m>=2 有原根当且仅当 m 具有下列形式之一：
其中 p为任意奇素数， k 为任意正整数。
首先我们做一个比较简单的工作：证明所有不满足 m=2,4,p^k,2p^k 的整数 m 都没有原根。分两步来证。
1.若大于等于 3 的两个整数 x,y 互素，则 xy 没有原根。
事实上，我们只需证明下面式子对于任意与 xy 互素的整数 a 成立就行了：
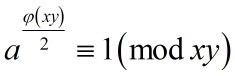
这样 a 模 xy的阶一定比 φ(xy) 小，也就不存在模 xy 的原根了。
注意到 x,y是互素的，所以我们只需证明这个同余式分别模 x,y 都恒成立就行了。而 a 的次方数显然是 φ(x) 的整数倍（因为 φ(y)是个偶数，从而 φ(y)/2 是个整数），由欧拉定理此式显然模 x 成立。同理此式模 y成立，于是这个式子就恒成立。
这个结论足以刨掉绝大多数的不满足 m=2,4,p^k,2p^k 的整数 m 。如果某个有奇素因子 p的整数有原根，那么将能整除这个数的奇素因子的最高次幂作为 x ，剩下的部分作为 y ，显然 x,y 是互素的，并且 x>=3，所以 y<=2 。这个数就只能是 p^k 或者 2p^k 。这样就只剩下了 m=2^k(k>=3)的情况没排除。
转载者对上面的解释：任意正整数均可以表示为2^m × p^k × p_1^k_1 × p_2^k_2 × …其中p、p_1、p_2为奇素数，m、k、k_1、k_2……≥0的整数
把上式中的p^k作为x，剩下部分作为y，
（1）对于m≥2，k≥1，k_1、k_2……≥0的情况，通过“若大于等于 3 的两个整数 x,y 互素，则 xy 没有原根”，进行了排除。
（2）对于m＜2，k≥1，k_1、k_2……＞0的情况，也通过“若大于等于 3 的两个整数 x,y 互素，则 xy 没有原根”，进行了排除。
（3）对于m＜2，k≥1，k_1、k_2……=0的情况，这个数就是 p^k 或者 2p^k 。
（4）对于这样就只剩下了 m=2^k(k>=3)的情况没排除。
2.若 k>=1 ，则 2^(k+2) 没有原根。
由于φ(2^(k+2))=2^(k+1) ，只需证明下面式子对于任意奇数 a 恒成立就行了：
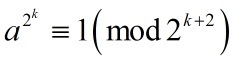
这样 a 模2^(k+2) 的阶一定比 2^(k+1) 小，模 2^(k+2) 的原根就一定不存在。
用归纳法可以很容易证明这个命题：当 k=1 时，显然所有奇数的平方模 8 余 1 。我们只要再证明
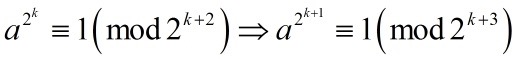
即可（证明格式写得不太正规…理解就行）。这个是很容易证的。
转载者注：由于a是奇数，那么a的任意次方也是奇数，奇数的表达式是a=2q+1，其中q是非负整数。如果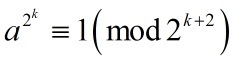成立，那么a^(2^k)就可以表示为下面的第一个等式。
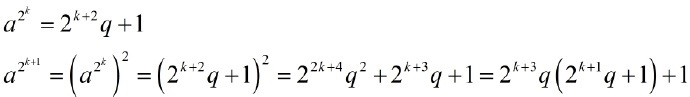
第二个式子写到最后就看出来了，它一定是 2^(k+3) 的某个整数倍加 1 。
至此我们就知道了：如果 m 不是 2,4,p^k,2p^k 中的任意一个，那么 m 不存在原根。
接下来我们验证，如果 m 是 2,4,p^k,2p^k 中的某一种形式，那么 m 存在原根。前两个当然好验证， 2 的一个原根是 1， 4 的一个原根是 3 。剩下两个就不太好办了。
我们先证明一个小结论：任意给定一个关于 x 的，最高次数为正整数 n的整系数多项式，且最高次项系数不是素数 p 的倍数，则满足条件的 x 的模 p两两不同余的取值最多有 n 个。或者换句话说，下面这个同余方程的模 p 两两不同余的解 x 最多有n 个：
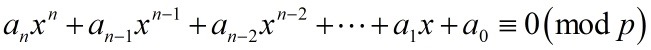
其中各项系数都是整数，且 a_n 不是 p 的倍数。
注意 p为素数这个条件不能去掉，否则有反例： x^2-1≡0(mod 8) 有 4 个模 8 不同余的解 1,3,5,7 。
证明采用归纳法。当n=1 时显然成立，此时方程化为 ax+b≡0(mod p) ，由 a,p 互素，显然它恰好有一个解。
设当 n=k时结论成立，当 n=k+1 时，任取一个满足前提条件的同余方程，如果它没有解，则显然满足“解最多有 n 个”的要求；否则它有一个解x_0 ，那么把左端的多项式（记为 P(x) ）除以 (x-x_0) 会得到一个次数为 k ，并且最高次项系数没变的多项式 Q(x)，还有一个余式 R(x) ：
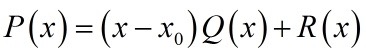
显然因为除式是个一次式，所以余式肯定是个常数 R（注：余式的阶要小于除式的阶） 。把 x=x_0 代到上面，左边是 p的倍数，那么右边的 R 也是 p 的倍数 。这样在模 p 意义下我们就可以把 R(x)扔掉，原先的方程 P(x)≡0(mod p) 就变成了 (x-x_0)Q(x)≡0(mod p) 。
3.任意奇素数 p 有原根。
然后我们来证明任意奇素数 p 有原根。首先有 φ(p)=p-1 。然后我们求出所有的 ord_p(a) ，其中 a 是 1 到 p-1的整数。这些数显然都是 p-1 的约数（可由欧拉定理立即得推论： φ(m) 是 ord_m(a) 的倍数），这样就得到它们的最小公倍数不大于 p-1 。再设这个最小公倍数为 L，则由指数的性质，得到对于所有 x=1,2,3,…,p-1 都有
换句话说，这个 L次同余方程有 p-1 个模 p 两两不同余的解。这样就证明了 L 一定不小于 p-1 。于是 L 只能等于 p-1 。
这也就是说，如果我们把 p-1 分解质因数：
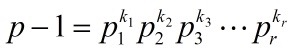
则在x=1,2,3,…,p-1中必然会有一个数模p的指数为 (p_1)^(k_1) 的倍数（注：p-1是所有指数的最小公倍数，所以p-1质因数分解中出现的p_1^k_1必然也会出现在某个指数的质因数分解中） 。设 a_1 模 p 的指数为 (p_1)^(k_1)的 t 倍，则由前面得到的结论可得 (a_1)^t 模 p 的指数等于 (p_1)^(k_1)。
类似地，我们可以分别找到模 p 的指数等于 (p_2)^(k_2),(p_3)^(k_3),…,(p_r)^(k_r) 的数，记为a_2,a_3,…,a_r 。又因为这里面所有 r 个指数都是互质的，可以把它们乘起来，即a_1*a_2*a_3*…*a_r 的指数就是 p-1 。这就找到了模 p 的一个原根。
如果上面两段写得不太清楚的话就看下面这个图吧。利用的是前面说过的指数的两个比较“高级”的性质：
我们利用这个结论进一步证明奇素数 p 的正整数幂有原根。
4.若 p 为任意奇素数， k 为正整数，则 p^k 有原根。
事实上我一开始找到一个规律：所有 p 的原根也是 p^2 的原根。然而后来写了个程序发现它是错的…举个反例。取 p=29 ，则14 是 p 的一个原根，但是 14^28≡1(mod29^2) ，这说明 14 不是 p^2 的原根。
不过，用 p的原根来构造 p^2 的原根，这种想法没有错。先看看最初的想法：我们试图证明所有 p 的原根也是 p^2 的原根，首先就要考虑两个关于x 的同余方程 g^x≡1(mod p) 和 g^x≡1(mod p^2) 。
我们知道第一个式子的最小正整数解为 p-1 ，而我们也可以发现，第二个式子的所有正整数解都是 p-1的倍数。这很简单，因为第二个式子的解也是第一个式子的解，而第一个式子的正整数解显然是 p-1 的倍数。
我们对第二个式子里的 x 换成 (p-1)t ，其中 t 是正整数，就可以对第二个式子变形：
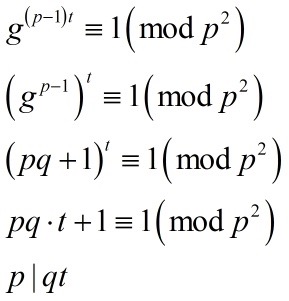
其中第三行是用g^(p-1) 除以 p ，得到商为 q ，由费马小定理余数一定为 1 。第四行是二项式展开得到的，而且把所有被 p^2整除的项都扔掉了，最后左边减右边，把同余式换成整除式，就得到 p|qt 。
我们知道，由于 p是个素数，一定可以得到 p 整除 q,t 中的一个。我们想要的是 p|t ，这样就可以倒推回去得出 g^x≡1(mod p^2)的指数 x 一定是 φ(p^2)=p(p-1) 的倍数。如果要是说明 p 不整除 q 就好了。而 p 整除 q 又意味着g^(p-1)≡1(mod p^2)
（注：如果p不整除q，那么只能是p整除t了，意味着x是φ(p^2)的倍数，所以x≥φ(p^2)，根据欧拉定理g^φ(p^2)≡1(mod p^2)，所以g就是p^2的原根。下面提到存在反例，需要调整证明方法。）
后来发现这个结论有反例，于是我们只能调整一下证明方法。我们知道 g 是 p 的原根，就意味着 g 加上一个 p 的倍数还是 p的原根。本来这些数都是模 p 同余的，没啥意思，但是如果模数换为 p^2 ，它们就有不同余的数了，我们在这些数里面找一找 p^2的原根。
从这些数里拿出一个，不妨记为 g+pk （ k 不能是 p 的倍数，否则这个数与 g 模 p^2 就一样了），我们考虑方程(g+pk)^x≡1(mod p^2) ，显然 x 仍然是 p-1 的倍数。那么我们不妨先把 (g+pk)^(p-1)展开一下：
我们立即得到：若g^(p-1)≡1(mod p^2) ，则立即得到 (g+pk)^(p-1) 模 p^2 的余数一定不是 1。否则我们会得到多出来的那一项 -g^(p-2)*pk 是 p^2 的倍数，但是 g,k 都不是 p的倍数，矛盾。如果事实是这样的话，我们用 g+pk 代替“其中第三行是用…”那句前面那张图里的 g ，再进行同样的推导，就有了 p不整除 q 。于是， g+pk 就是 p^2 的一个原根。
（注：通过g和g+pk都是p的原根，但g^(p-1)≡1(mod p^2) 和(g+pk)^(p-1)≡1(mod p^2)不能同时成立，可以证明p不整除q。同理：那么只能是p整除t了，意味着x是φ(p^2)的倍数，所以x≥φ(p^2)，根据欧拉定理(g+kp)^φ(p^2)≡1(mod p^2)，所以g+kp就是p^2的原根。
接下来我们继续说明，上面构造出的 p^2 的一个原根（不管是 g 还是 g+pk ）同样也是p^3,p^4,p^5,…的原根。我们下面为了简便起见，就把这个原根当作是 g （因为这个原根的构造方法究竟是 g 还是 g+pk，对我们来说已经没用了）。
我们记g^(p-1)=pq+1 ，把这个式子两端不断取 p 次方就可得：
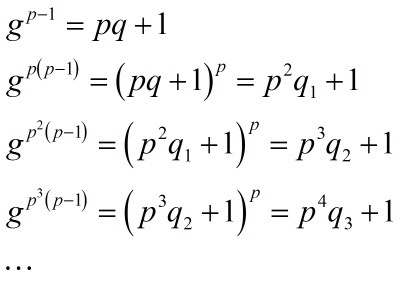
每次都要利用二项式定理。我们不仅可以推出 q_1,q_2,q_3,…都是整数（事实上，这个由欧拉定理直接就出来了，因为指数上是p^k 的欧拉函数），而且可以推出它们不是 p 的倍数。先拿第二行式子举个例子，我们只关心倒数三项（剩下的项中 pq的幂至少是 3 次，一定是 p^3 的倍数，它不会改变 q_1 是否被 p 整除的）。
注：q_1是关于p和q的多项式，其中含有p的项必然是p的倍数，所以q_1是否是p的倍数不取决于这些含p的项，而这些含p的项就是来自于二项式展开后那些含有p^3的项。
稍加思考会发现，因为指数p是个质数，所以除了两头的 1 之外，所有的二项式系数都是 p的倍数，而倒数第三项肯定不是两头的 1 （注意，这里利用了 p 是奇质数的条件，如果 p=2则倒数第三项就是第一项，它的二项式系数就是 1 了），所以倒数第三项可以利用 pq 的二次方和二项式系数中的 p凑成三次方，于是我们不用再看倒数第三项了。
而最后两项写出来就是 p^2*q+1 ，立刻可以看出被 p^2 除的余数为 1 （所以 q_1 是个整数），并且既然 q 不是 p的倍数，那么 q_1 也不是 p 的倍数。后面的几个式子同理，也是只看最后两项。
注：通过推导可知q_1=np+q，因为q不是p的倍数，所以q_1也不是p的倍数。
注意到每行 g的指数都是形如 p^k 的欧拉函数，我们考虑同余式 g^x≡1(mod p^k) 的正整数解 x 。显然 x 必须是 p-1的倍数（因为 g^x≡1(mod p) ），另外如果取最小的正整数解 x ，它就必然是 φ(p^k)=p^(k-1)*(p-1) 的约数。这样最小正整数解就只能是 p^t*(p-1) 的形式。
又由于刚才的结论，g^[p^t*(p-1)]=p^(t+1)*q_t+1 ，因为 q_t 不是 p 的倍数，不能靠它提供素因子 p，而且要保证这个数是 p^k 的某个倍数加 1 ，只能让 t+1 不小于 k 。这样，就得到 x>=p^(k-1)*(p-1) （注：通过推导出的g^[p^(k-1)*(p-1)]=p^k*q_k，可知只有x>=p^(k-1)*(p-1)，才能保证右侧的p的次方大等于k），也就是说 x 的最小正整数解恰好就是 φ(p^k) 。
注：通过同余式 g^x≡1(mod p^k) ，可知x是 φ(p^k)=p^(k-1)*(p-1) 的约数。通过对式子g^(p-1)=pq+1两端不断取 p 次方推导出的公式，可知x>=p^(k-1)*(p-1)，所以x的最小正整数解恰好就是 φ(p^k) 。
这样，我们终于对任意奇素数 p 和任意正整数 k ，找到了 p^k 的原根。最后一步还是比较简单的：
5.若 p 为任意奇素数， k 为正整数，则 2p^k有原根。
由上面的讨论， p^k 一定存在原根 g 。我们可以不妨设它是奇数，否则我们就用 g+p^k 代替 g （这两个数是模 p^k同余的）。我们证明 g 是 2p^k 的原根。
首先我们有φ(p^k)=φ(2p^k) ，这里不写出具体值，因为没啥用。满足 g^x≡1(mod 2p^k) 的正整数 x 一定不小于φ(p^k) ，因为它一定满足 g^x≡1(mod p^k) 。另外，由欧拉定理 x=φ(p^k) 也可以是上述方程成立。这就说明了φ(p^k)=φ(2p^k) 是 g 模 2p^k 的指数， g 是模 2p^k 的一个原根。
终于说完了……可能有点啰嗦。不过最后一个小结论却很简单，也很好证：
若整数 m>=2 有原根，则它在 0,1,2,3,…,m-1 里与 m 互素的数中有 φ(φ(m))个原根。
证明太简单了，不是说它有原根吗？我们随便取一个原根 g 出来，这样 0 到 m-1 中所有与 m 互素的数可以重新排列成g^0,g^1,g^2,g^3,…,g^(φ(m)-1) （模 m 意义下）（注：因为g是m的原根，所以g模m的指数等于φ(m)，所以前面各数互不相同 ） 。我们前面提到过，这里 g 的次数 k 可以叫做对应g^k 的指标。容易看出，当且仅当指标与 φ(m) 互素时它是个原根。
原数取某次方等于指标乘以这个倍数，如果指标与 φ(m) 互素，那么指标至少乘以 φ(m) 它才能是 φ(m)的倍数。否则，指标与 φ(m) 不互素，那么指标乘以某个比 φ(m) 小的正整数也可以变成 φ(m) 的倍数。
这就简单利落地证明了原根有 φ(φ(m)) 个。好了，说的够多了，下次该进入平方剩余的世界了…