作者:氯化钡和硫酸银
时间:2014年2月3日 11:14
来源:http://blog.sina.cn/dpool/blog/s/blog_a661ecd50101ax02.html
最近弄到一本电子书,《数论概论》,感觉这本书写得非常棒…先从简单的开始。
费马小定理
费马小定理的内容如下:若 p 为素数,整数 a 与 p 互素,那么有
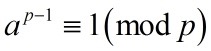
看着很简单吧。它的证明也非常巧妙。
我们考虑1,2,3,…,p-1 这 p-1 个数,将它们同乘以 a 得到 p-1 个数 a,2a,3a,…,(p-1)a。考虑一些小的例子,我们很容易猜想这 p-1 个数分别与 1,2,3,…,p-1 同余(模 p,次序可能不同)。
我们只需证明这两件事:
1.它们均不是 p 的倍数; 2.它们两两模 p 不同余。
第一项的证明简单,因为如果某一项 ka 是 p 的倍数,则 p 必定整除 k,a 中的一个,但是事实上这两个都不是 p 的倍数( a与 p 互素, k 是 1 到 p-1 的整数),矛盾。所以这些数都不是 p 的倍数。
第二项的证明也不难。若某两项 ka,la 模 p 同余,则 p 被它们的差(k-l)a整除 , p 必定整除k-l,a中的一个,但是事实上这两个都不是 p 的倍数( a 与 p 互素, |k-l| 是 1 到 p-2 的整数),矛盾。
于是,这 p-1个数除以 p 的余数只可能分别是 1,2,3,…,p-1,尽管次序可能不同。这样的话,利用多个同余式可以相乘的性质(以及乘法交换律),就可以得到:
![]()
两边有一个公因子,把它约掉我们就证完了。别急,先看看能不能约:可以约分的条件是 p 与要约掉的公因子互质。这里公因子是 (p-1)!,它显然不被素数 p 整除,也就是说它与 p 互素。这样就证完了。
还有一种证法,用到了二项式定理。设 p 为质数,则由二项式定理得:
![]()
然后,可以证明C(p,k) 是 p 的倍数(其中 k 是 1 到 p-1 的整数)。证明很简单,把它用组合数公式写开就是:
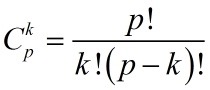
显然分母上没有因数p ,这样分子上的 p 约不掉,整个分数就是 p 的倍数。
现在设上面二项式定理中的 a,b 为整数,再模 p 就得到:
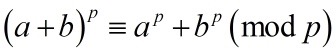
这个式子很简洁,它可以推广到多个底数的情况。大家都知道,一般的二项式定理推广到多元时形式很复杂,但是在这里就很简单:
![]()
这只需对左边用n-1 次二元的定理即可。现在我们只差最后一步,把所有的 a_i 都取为 1 ,并设有 a 个 1 ,就得到:
![]()
又因为 a 与 p 互素,两边约掉一个 a 就完成任务。
欧拉定理
欧拉定理是个费马小定理的推广,把素数模数推广为任意正整数。若整数 a 与正整数 m 互素,则有
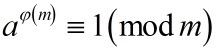
其中 φ(m)表示在 1,2,3,…,m 中与 m 互素的整数的个数(也叫做欧拉函数)。(互素的定义:两个数的 “最大公约数”是1。)
注:φ(m)=1,欧拉定理两侧mod 1后,均为0,等式依然成立。
既然先说了欧拉函数的定义,我们就用它来把费马小定理的第一个证明变化一下。把 1,2,3,…,p-1 这些数换为在1,2,3,…,m 中与 m 互素的整数,共有 φ(m) 个,再把它们同乘以 a 后,新得到的这 φ(m)个数应满足这两个性质:
1.它们均与 m 互素; 2.它们两两模 m 不同余。
第一个简单,因为两个与 m 互素的整数相乘仍然与 m 互素(这是个很直观的结论,因为找不到大于 1的公因子。互素的本质:两个数分别做质因数分解,二者没有共同的质因数。)。第二个也好证,如果两个数 ka,la 模 m 同余,则 m 整除 (k-l)a ,而由 (a,m)=1 得 m 必定整除k-l ,这显然是不成立的,因为后者的绝对值一定小于 m 。
这样,这 φ(m)个数除以 m 的余数必然一一对应于 1,2,3,…,m 中与 m互素的整数(次序可能不同。因为:互素的两个数相除,余数必然与除数互素,可以采用反证法证明,如果余数与除数不互素,那么除数与被除数必然不互素,即存在相同的质因数。),接下来只需照葫芦画瓢即可:
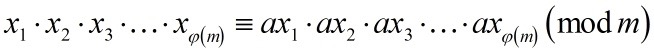
其中 x_i表示在 1,2,3,…,m 中与 m 互素的 φ(m) 个整数,既然它们与 m互素,那么把它们从同余式两边约去,欧拉定理就证完了。
顺便说一句,因为对于素数p ,有 φ(p)=p-1 (显然 1,2,3,…,p-1 与 p 互素),因此费马小定理可以称为欧拉定理的一个特殊情况。
威尔逊定理
刚才的两个定理描述的是整数的某个特定的幂,而威尔逊定理则着眼于阶乘。设 p 为素数,则有:
![]()
(没准 C++的同志们会以为是不等号…)
证明它有个简单易懂的方法:配对。其实在等差数列求和的时候就可以用这种方法:据说高斯上小学的时候算出了1+2+3+…+100,方法是这样的……这个都知道吧。我们用所谓“倒序相加”法代替了配对,避免了奇偶讨论,不过在这里要防止开方的麻烦,我们还是用配对法。
因为这里是相乘,最好能找到两个数的乘积除以 p 余 1 ,把它们配对可以减少运算量。还好我们有这个结论:
对于 1,2,3,…,p-1 中的任意一个数 a ,在 1,2,3,…,p-1 中恰有一个数 b 使得 ab 被p 除余数为 1 。
把 b 称作 a模 p 的数论倒数,用 a^(-1) 表示(当然在 p 不是质数时也可类似定义数论倒数,不过要求 a,p互素)。这个结论其实我们已经证过,刚才证明费马小定理时,把 1,2,3,…,p-1 同时乘上 a ,它们除以 p的余数必然有且仅有一个为 1 ,它对应的 a 的倍数就是满足条件的 b 。
显然, a 也是b 模 p 的数论倒数。
下面我们就开始配对了。考虑集合 {1,2,3,…,p-1},首先从中任选一个数,并且将它连它的数论倒数一起拿出来成对(也可以说这两个数互为数论倒数,正如相反数一样);然后再任选一个数,将它和它的数论倒数一起拿出来成对,……,直到集合里没有元素。
当然这里假设 p为奇素数(这样才可以一对一对),可以先对 p=2 时验证一下,发现威尔逊定理成立,后面就设 p 为奇素数。
稍等一下,下面的两个问题关系到这种配对能否进行:从集合里随便取一个数,
1.它的数论倒数会不会已经取过而不能配对?
2.它的数论倒数会不会是它自己?
对于第一个问题,答案是不会,因为如果出现这样的情况,这个数的数论倒数就可以同时与两个数配对,违反了数论倒数的唯一性。
对于第二个问题,这个是可能的,比如 1 的数论倒数就是它自己。事实上, p-1 的数论倒数也是它自己。不过还好,容易证明在1,2,3,…,p-1 中这种数只有这两个:
若 x的数论倒数是它自己,则 x^2 被 p 除的余数为 1 ,因此 p 整除 x^2-1 即 (x+1)(x-1) ,又由于 p为素数,则 p 必定整除 x+1,x-1 中的一个,整除前者则 x=p-1 ,整除后者则 x=1 。
这样,我们的配对策略只需稍加修改即可:先把 1,p-1 两个数拿出来,剩下的数就不存在那两个问题,可以顺利配成 (p-3)/2对。每对乘积模 p 都余 1 ,不用管它们,起作用的是 1,p-1 两个数,它们的乘积模 p 为 -1。这样威尔逊定理就证完了。
最后简单提一下,这个定理反过来说,设 p>1 为满足 (p-1)!≡-1(mod p) 的正整数,则 p 一定是个质数。
证明很简单,如果p 为合数,那么不妨设 p=ab ,其中 a,b 均大于 1 小于 p 。当 a,b 不同时显然 p 能整除 (p-1)!(因为有这两个因数)。当 a,b 相同时,只要 a>2 ,那么 (p-1)! 中含有 a,2a 两个因数,同样有 p 整除(p-1)! 。若 a=b=2 ,则 p=4 ,代入验证一下发现 (p-1)!≡2(mod p) 也不对。
这个定理是一个判断素数的很准确的算法,不过由于我们不能有效地计算阶乘(计算幂可以用快速幂等方法有效计算),因此实际上没人用这个算法。
中国剩余定理
中国剩余定理研究的是同余方程组,内容如下:
设
![]()
是 n 个两两互质的正整数(可以设为大于 1,因为如果有 1 的话这个数相当于废的),则下列关于整数 x 的方程组
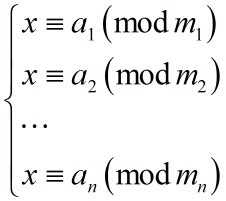
恰有一个解满足
![]()
也就是说,如果知道一个整数分别除以 n个两两互质的除数的余数,那么这个整数除以全部除数的积的余数也是唯一确定的(并且一定存在)。
看起来这个定理很麻烦,其实要证它只要会数数就行了…还用到乘法原理。
首先我们把所有m_i 的乘积记为 M ,先数一数满足 0<=x
然后,我们再数数如果把每个整数都分别除以 n 个除数 m_i (并且把 n个余数看作是一个数组),会产生多少种情况。这个容易通过乘法原理数出来,第 i 个余数有 m_i 个不同的取值,那么总情况数就是 M。
接下来我们证明关键的一个结论:满足 0<=x
使用反证法很容易证,假设在 0<=x
这样就只有一种可能性:满足 0<=x
还有一种证法用的是构造的思路。没错,这种问题也可以构造,我们想办法构造出一个整数,使得它除了被第一个除数除余数为 1外,其它的除数都能整除它。类似地,我们把“第一个除数”换成“第 i 个除数”,可以构造出 n个这样的整数,然后解同余方程的时候,我只需让 a_1 乘以第一个整数, a_2 乘以第二个整数,……, a_n 乘以第 n个整数,把它们加起来,再除以所有除数的乘积 M 就行了。
找出 n个这样的整数要简单地多。构造第一个时,我们很容易得出它被 M/m_1 (也就是除了第一个除数之外,其它所有除数的乘积)整除,而它被m_1 除的余数是 1 。用裴蜀定理可以很容易证明存在这样的数,不过不知道那个定理也不要紧,我们把 1,2,3,…,m_1-1这些整数全部乘以 M/m_1 ,然后证明这些乘积除以 m_1 的余数两两不同并且不为 0 (由于 m_1 与 M/m_1互素,这是很容易证的)。这样,这些乘积中必然有一个除以 m_1 的余数为 1 。这个数就是我们要找的。
————————————————
来自百度百科


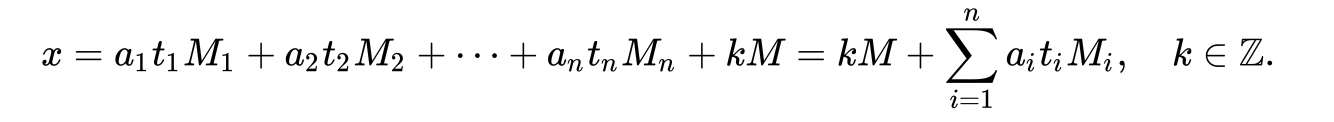

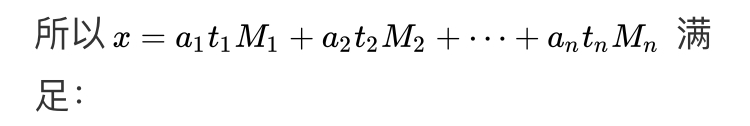
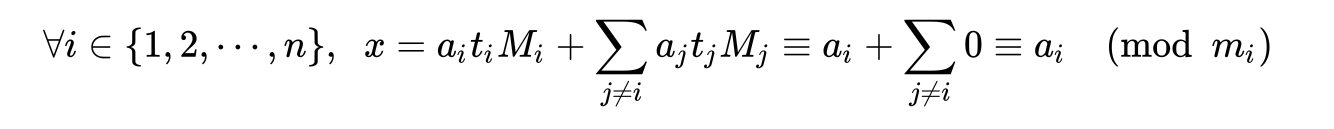

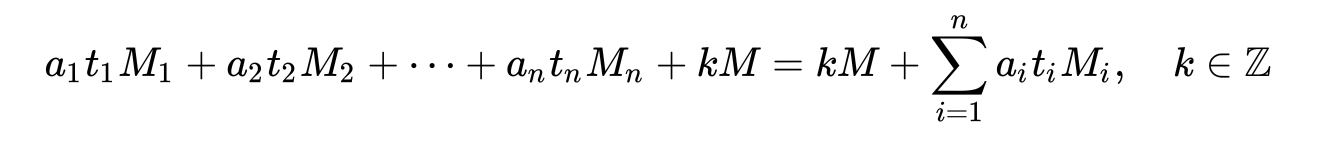

顺便提一下,这个定理被命名为“中国剩余定理”或者“孙子定理”是因为中国古算书《孙子算经》上有个问题:
有物不知其数(shù),三三数(shǔ)之余二,五五数(shǔ)之余三,七七(shǔ)数之余二,问物几何?
后来就有人编了首诗,它可以解决模 3,5,7 的同余方程组问题:
三人同行七十稀,五树梅花廿一枝,
七子团圆正半月,除百零五便得知。
注意 70 恰好被5,7 整除,被 3 除余数为 1 ,同理后面的 21,15 也是这么来的。只要除数不变,这三个数就可以用。最后除以 105当然是为了保证结果在 0~104 范围内。
由于M=3×5×7=105
那么通解则是
x=2×70+3×21+2×15 + k×105 (k是任意整数,所以可以是负整数)
那么mod M的唯一解,则是
x=(2×70+3×21+2×15) mod 105=23