中本聪的天才：比特币以意想不到的方式躲开了一些密码学子弹

说到开源协议，比特币的独特之处之一在于它的协议极难做出调整。不像其他的协议，特性可以在一瞬间就完成增加、修改、或者废弃的动作，在比特币的世界里，就算是最轻微的改动也需要整个比特币网络中的绝大多数同时合作。原因很简单：比特币世界，并且只在比特币世界，要求完全的共识。在像HTML和CSS这样的因特网协议里，如果一个网页浏览器错误的解析了一些样式元素，能发生的最糟糕的情况也就是页面渲染不正确。而在比特币这，单单一笔交易被错误的判断成有效或者无效就会让整个块失效，并可能像2013年3月的那次那样，引起整个网络的一分为二。所以，中本聪在2008年做出的绝大多数决策我们都坚持着。尽管中本聪的选择绝对不是完美的，但幸运的是他正确的次数经常比错误要多；事实上，有几个实例，因为中本聪的选择我们获得了更好的结果，而更好结果的原因可能中本聪自己都没想到过。

比特币地址是公钥的哈希值

比特币有有趣的方面之一（对很多人来说可能最开始都有点迷惑），是私钥和比特币地址直接的精准的关系。你把交易发送到一个“比特币地址”，并且声明这笔花出去的交易需要一个相对应的“私钥”的签名。但这两个值之间的关系是怎么样的呢？在一个普通的公钥签名系统里面，步骤如下：

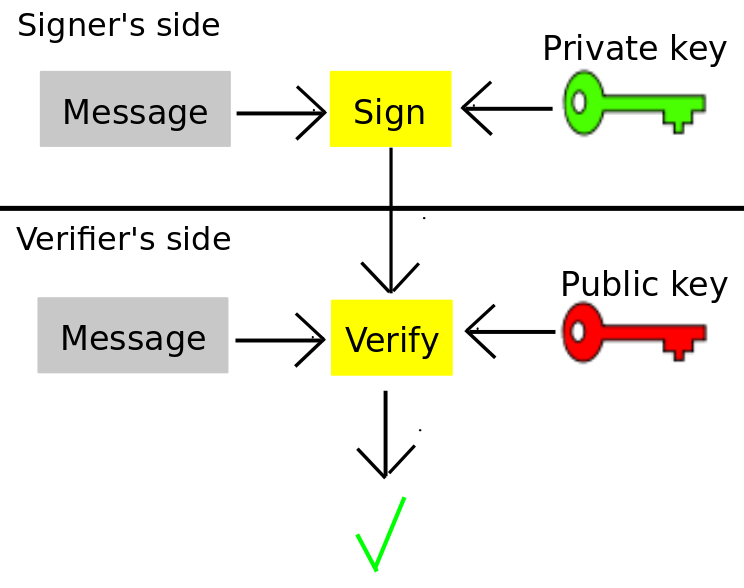
有一个产生密钥对的算法，密钥对由一把公钥和一把私钥所组成，这样私钥可以用于为消息生成签名，公钥可以用于验证那个签名。这样的意义是什么？一般来讲，私钥的持有着希望证明他们亲自写出了或者授权了一条特定的消息。如果除了私钥持有着之外的某个人想要制造一个签名，那么和相对应的公钥的验证就会失败。如果消息在传输过程中被修改，验证同样也会失败。人们可以看到这个机制可以如何的在像比特币这样的货币中被使用：每个人公开他们的公钥，从A发送到B需要A用他的私钥签名一条包含了B的公钥的消息。自此，协议可以推断A想要发送一笔钱给B。

然而，比特币是更加复杂的。比特币的地址不是公钥，而是公钥的哈希值。哈希是一个函数，它可以把任何东西都做输入，并产生一个固定长度的输出，并且此流程基本上不能被反转过来。也就是说，给出一条消息M，计算M的哈希值（hash(M)）是很容易的，但给出hash(M)想要找到M却是直到世界毁灭也不大能完成的事情。比特币的私钥和地址的关系如下：

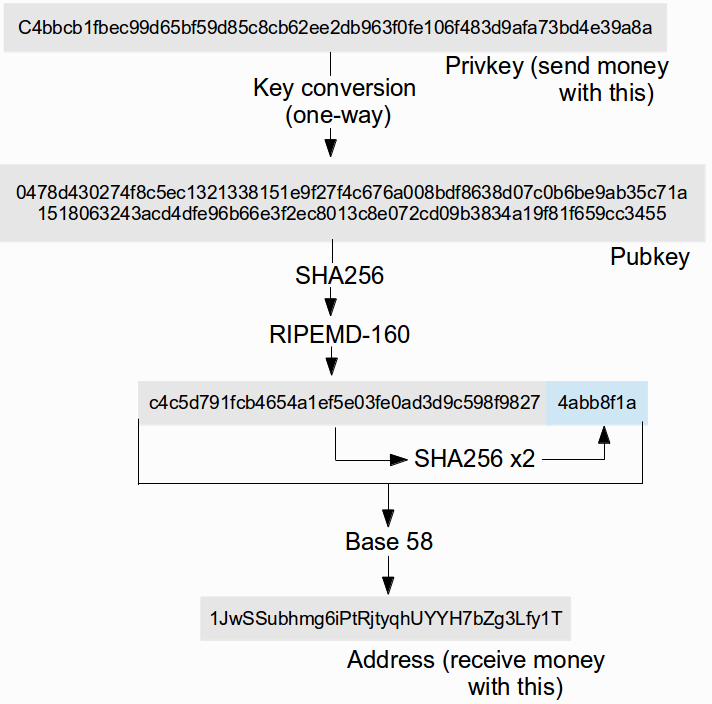
所以交易是如何工作的呢？除了除了关于交易本身的明显信息以外，一笔比特币交易包括了两个东西：花费者的公钥、以及用花费者的私钥做出的签名。任何一个验证这笔交易的人都需要检查：（1）这个公钥的哈希值是花费者的地址；（2）签名可以用公钥验证通过。把它们放到一起，这些就是交易是由相对应与花费者的地址的私钥的拥有者自己（或者授权他人）进行的。

这点的意义平凡到让人惊讶：在比特币使用的椭圆曲线数字签名算法加密系统里面，一个公钥有512位长度，意味着它需要接近100个字符来呈现。举个例子，下面是一个公钥：

04b52fd5a616a8f08ccad58469102f86fc7891e5aa4262ab8d43e41767c17d45b

80850044a62af51783609176daf02fc46221057a8de11ee6ae8743065b27a4b5e

与此同时，它对应的十六进制形式的比特币地址如下：

4b463093e6fc3135a4de2ff577c4b658198777a9

人们更加熟悉的base58编码形式的是：

1obodiqhAZ3GD9onBXRZ9v7hshkuBreCu

然而，在现实里，。最后发现，有一种以更紧凑的形式编码公钥的方法，只需要257个字节（译者注：这里好像有点问题，应当是257位，参见此文http://618.io/blog/2013/07/30/bitcoin-basic/）：

03c5c9833d00bed3211a5f3733316ecf6ebc407806d70caa14862f1e2e8c2f852d

如果我们决定把它变成base58编码的形式：

15sqRCowBDTfyuxPQD3ba8sN3wBB8MwGbo6gsBEGeKmUbNQADGh

比我们如今使用的地址也没长多少。所以中本聪的选择只是带来了不必要的复杂度和浪费吗？最后证明，答案是否定的。有另外一个非常好的理由去使用这个“公钥的哈希值”的地址结构：量子加密技术。量子计算机可以破解椭圆曲线数字签名算法（也就是说，给定一个公钥，量子计算机可以相当快速的找到对应的私钥），但它们不能相类似的逆转哈希算法（或者说他们可以，但是将需要花掉2⁸⁰个步骤来完成一个比特币地址的破解，这仍然是相当不可行的）。因此，如果你的比特币资金存放在一个你没有支出过的地址里（这意味着公钥是没有公开的），它们在量子计算机面前也就是安全的，至少在你把它们花掉之前。有理论上的途径可以让比特币完全免于量子计算机的威胁，但一个地址只是一个公钥的哈希值的事实，意味着一旦量子计算机真的出现了，在我们全面切换之前攻击者可以造成的损失要小得多。

2100万总币数的限制

比特币有争议的属性之一就是它的固定的供应量。当前每10分钟又25个新的比特币被生产出来，并且这一数字每4年减半。总的来讲，不会有超过2100万个比特币的存在。另一方面，每个比特币可以被划分成1亿份（每份叫做1“聪”），如果一美分都足够买辆车的话，用美元来交易就麻烦重重了，但比特币就算升值到和上面假设的美元的状况，也不会遇到那样的问题。因此，总之，将永远存在的货币单位的总数字是2,100,000,000,000,000，也就是2100万亿，或者说2^50.899。在选择这个数值的方面，中本聪比大多数人意识到的要幸运的多或者说聪明的多。首先，这个数字远小于2⁶⁴-1，这是一台计算机里面可以以标准整数形式存放的最大整数，超过那个值的话，数值将像里程表那样归零。

其次，然而，还有一个总“聪”数要设法低于的更小的阈值：可以用浮点的格式表示的可能的最大整数。整数不是计算机可以存储的唯一一种数字；为了处理小数，计算机使用一种做浮点表示法的格式。浮点表示法本质上就是一个科学记数法的二进制版本。举个例子，下面是一个在你学习物理学的时候会遇到的值：

• 地球的质量: 5.972 * 10²⁴ kg
• 太阳的质量: 1.989 * 10³⁰ kg
• 光速: 2.998 * 10⁸ m/s
• 一光年: 9.460 * 10¹⁵ m
• 质子的质量: 1.672 * 10^-27 kg
• 普朗克长度: 1.616 * 10^-35 m

我们可以注意到，科学记数法是如何使得你可以在合理的精度下表示所有的这些数值，尽管它们的大小相差极大。浮点表示法本质上就是二进制的科学记数法；当你存储数字9.625的时候，你的计算机存放的是“1.001101 * 10¹¹”（或者说，它存放的是01000000 00100011 01000000 00000000 00000000 00000000 00000000 00000000，这是高精度序列形式的同样一回事）。在这个高精度形式中，系数（也就是不是指数的那部分）有52位（52bits）。这意味着高精度（更加精确的说法是“双精度”）浮点数足以存贮高达2⁵³的数字，但不能再高了，如果超过了，你就得开始砍掉末尾的数字。比特币的2^50.9这一以指数形式表现的总“聪”数，刚好低于这个最大值。

如果我们有了整数，我们为什么还要关心浮点值呢？因为更多的高阶编程语言（比如说Javascript）并不开放低阶的“浮点”和“整数表示法”，而只给程序员提供“数”的概念 – 当然以浮点的形式提供。如果中本聪当时选择了2亿1千万而不是2100万这个值的话，用很多语言里比特币编程就会比现在要麻烦得多了。

注意，Stefan Thomas不幸的在他写BitcoinJS的时候没有及时留意到这个，以至于那个库使用了一个专门的‘大数big number’对象，而不是一个普通数来存储教程输出值；我自己分叉的的BitcoinJS（同时还加入了其他的改进）使用了普通数。

选择正确的椭圆曲线

椭圆曲线加密算法不是一个单独的标准化的加密 消息的方法；事实上有许多不同的“曲线”可供选择。要想理解不同的“曲线”是什么，首先对椭圆曲线加密算法背后的数学原理有一个基本的了解是很有帮助的。总的来讲，一条椭圆曲线是由等式y² = x³ + ax + b（a和b都是曲线的参数）上的一系列的点（x,y）所组成。下面是一条椭圆曲线：

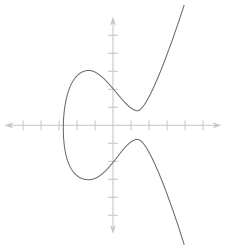
椭圆曲线加密算法依赖于叫做“点加”和“点乘”的在曲线上的运算，下图能做最好的诠释：

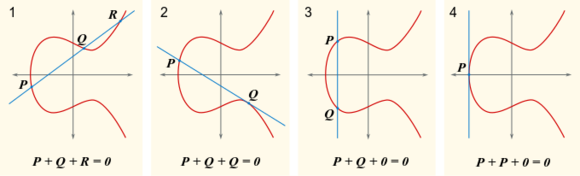
简单讲，想要把P和Q两点相加，就在两点之间画条线，找到这条线和曲线相交的第三个点，然后从那个点话垂直线以得到你的答案。然而，这些曲线有个弱点：它们是不精确的。如果你进行了多次的点加，浮点四舍五入带来的差错就会慢慢的累积，并最终导致结果成为一个没有意义的噪音。因此，椭圆曲线加密算法用了一条修改了两个地方的椭圆曲线。首先，等式现在是 y² = x³ + ax + b + kp，k可以使任何整数而p是大的素数（除了a和b的曲线参数）。其次，x和y必须是整数。尽管最后出来的结果几乎不是一条“曲线”，但也在数学上够用了，并且限制在整数避免了四舍五入带来的偏差。

有许多不同的曲线参数可以被使用；SEC2文档就提供了一个标准的。然而，一般而言，曲线会被分成两类：“伪随机”曲线以及Koblitz曲线。在一条伪随机曲线里，参数a和b是从某个“种子”通过一个特定的算法（本质上是哈希运算）来选择。对于secp256r1（这是标准256位伪随机曲线）来说，它的“种子”是c49d360886e704936a6678e1139d26b7819f7e90，产生的参数是：

p = 115792089210356248762697446949407573530086143415290314195533631308867097853951

a = 115792089210356248762697446949407573530086143415290314195533631308867097853948

b = 41058363725152142129326129780047268409114441015993725554835256314039467401291

一个显眼的疑问：这个种子是怎么来的？为何这个种子不是其他某个看起来更加单纯的数字，比如说15？最近揭露的关于美国国家安全局颠覆加密标准的消息中，一个很重要的点就是说这个种子是以某种方式精心选择的，为了以某种只有国安局知道的方法来弱化这条曲线。谢天谢地，回旋余地不是无限的。因为哈希函数的特性，国安局不能先找到一条“弱”曲线然后再去确定种子；唯一的攻击途径是尝试不同的种子，直到最后有一个种子产生了一条“弱”曲线。如果国安局知道知道一个只能影响一条特定曲线的椭圆曲线的漏洞，那么伪随机数参数的产生流程将阻止他们把那个漏洞标准化推广到其他曲线。然而，如果他们发现了一个通用的漏洞，那么那个流程也就不能提供保护了。我们都知道，c49d360886e704936a6678e1139d26b7819f7e90有可能是美国国家标准技术局尝试过的第10亿个种子。

幸运的是，比特币使用的不是伪随机曲线；比特币使用了Koblitz曲线。比特币的secp256k1的参数如下：

p = 115792089237316195423570985008687907853269984665640564039457584007908834671663

a = 0

b = 7

就是这样。并且甚至p都是很容易得出来的；它只是2²⁵⁶ – 2³² – 977（公平的说，p和a在secp256r1里面也是相当简单的；它的问题出在b）。这些参数的简约，使得国安局和国家标准技术局没有精心创造一条邪恶曲线的余地。并且甚至0、7、还有977这些数值的采用都是基于安全和效率的考虑而采用的。当Dan Brown，他是高效密码学组标准的现任主席，被问及此事时，他回复说：“我不知道比特币正在使用secp256k1。确实，我对于有人会采用secp256k1而不是secp256r1感到惊讶。”如果secp256r1是事实上的被破解了，那么因为比特币是为数不多的几个采用secp256k1而不是secp256r1的程序，比特币真的是躲过了一颗子弹。

原文 http://bitcoinmagazine.com/7781/satoshis-genius-unexpected-ways-in-which-bitcoin-dodged-some-cryptographic-bullet/

作者 Vitalik Buterin

翻译 He1l_Q

本文如有帮助，请考虑捐助：15X9AMhccjqqPRkhpgraoj7fgdqymW3iSC

欢迎转载，转载时请注明作者翻译者和出处，谢谢支持！