网络来源:百度百科
生日悖论
生日悖论,指如果一个房间里有23个或23个以上的人,那么至少有两个人的生日相同的概率要大于50%。这就意味着在一个典型的标准小学班级(30人)中,存在两人生日相同的可能性更高。对于60或者更多的人,这种概率要大于99%。从引起逻辑矛盾的角度来说生日悖论并不是一种悖论,从这个数学事实与一般直觉相抵触的意义上,它才称得上是一个悖论。大多数人会认为,23人中有2人生日相同的概率应该远远小于50%。计算与此相关的概率被称为生日问题,在这个问题之后的数学理论已被用于设计著名的密码攻击方法:生日攻击。
悖论内容
著名的生日悖论
23个人里有两个生日相同的人的几率有多大呢?
居然有50%
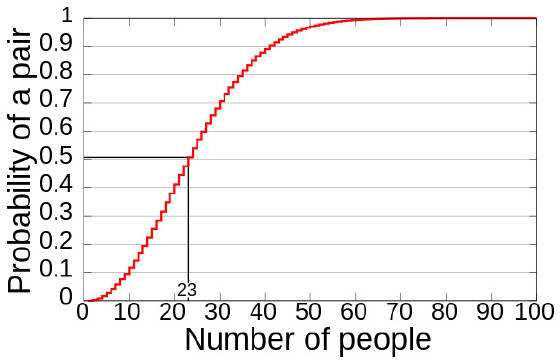
问题是这样的: 如果一个房间里有23个或23个以上的人,那么至少有两个人的生日相同的概率要大于50%。这就意味着在一个典型的标准小学班级(30人)中,存在两人生日相同的可能性更高。对于60或者更多的人,这种概率要大于99%。
不计特殊的年月,如闰二月。
先计算房间里所有人的生日都不相同的概率,那么
第一个人的生日是 365选365
第二个人的生日是 365选364
第三个人的生日是 365选363
:
:
:
第n个人的生日是 365选365-(n-1)
所以所有人生日都不相同的概率是:
那么,n个人中有至少两个人生日相同的概率就是:
所以当n=23的时候,概率为0.507
当n=100的时候,概率为0.999999692751072
对于已经确定的个人,生日不同的概率会发生变化。下面用随机变量计算:
令X[i,j]表示第i个人和第j个人生日不同的概率,则易知任意X[i,j]=364/365
令事件A表示n个人的生日都不相同
P(A)=
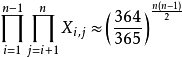
解P(A)<1/2,由对数可得:n>=23
相比之下,随机变量也同样的简单易懂
,且计算起来要方便得多。
理解悖论
理解生日悖论的关键在于领会相同生日的搭配可以是相当多的。如在前面所提到的例子,23个人可以产生23 × 22/2 = 253种不同的搭配,而这每一种搭配都有成功相等的可能。从这样的角度看,在253种搭配中产生一对成功的配对也并不是那样的不可思议。
换一个角度,如果你进入了一个有着22个人的房间,房间里的人中会和你有相同生日的概率便不是50%了,而是变得非常低。原因是这时候只能产生22种不同的搭配。生日问题实际上是在问任何23个人中会有两人生日相同的概率是多少。
悖论应用
生日悖论普遍的应用于检测哈希函数:N-位长度的哈希表可能发生碰撞测试次数不是2^N次而是只有2^(N/2)次。这一结论被应用到破解cryptographic hash function的生日攻击中。
生日问题所隐含的理论已经在[Schnabel 1938]名字叫做capture-recapture的统计试验得到应用,来估计湖里鱼的数量。
悖论定义
悖论是指一种导致矛盾的命题。悖论(paradox)来自希腊语“para+dokein”,意思是“多想一想”。 如果承认它是真的,经过一系列正确的推理,却又得出它是假的;如果承认它是假的,经过一系列正确的推理,却又得出它是真的。
把集合分成两类,凡是不以自身作为元素的集合称为正常集,(例如,自然数集N本身不是一个自然数,因此N是正常集。)凡是以自身作为元素的集合称为异常集。(例如,所有的非生物的集合F也是非生物,因此F是异常集。)
这样,许多日常中常见的悖论(说谎者悖论,理发师悖论,上帝悖论等)都可以归入异常集之中了。
另外一种悖论是关于无限的,虽然我们基本上都能接受极限的理论,但是要把这个理论向那些不懂的人解释还是十分困难的。
经典故事
(古希腊数学家芝诺(Zeno of Elea)的阿基里斯悖论)阿基里斯在赛跑中不可能追上起步稍微领先于他的乌龟,因为当他要到达乌龟出发的那一点,乌龟又向前爬动了。阿基里斯和乌龟的距离可以无限地缩小,但永远追不上乌龟。
(古希腊数学家芝诺(Zeno of Elea)的二分法悖论)当一个物体行进一段距离到达D,它必须首先到达距离D的二分之一,然后是四分之一、八分之一、十六分之一、以至可以无穷地划分下去。因此,这个物体永远也到达不了D。
“1厘米线段内的点与太平洋面上的点一样多”
康托尔(1845-1918)成功地证明了:一条直线上的点能够和一个平面上的点一一对应,也能和空间中的点一一对应。由于无限,1厘米长的线段内的点,与太平洋面上的点,以及整个地球内部的点都“一样多”。