时间:2021年6月22日 23:12:30
来源:https://blog.csdn.net/u013182438/article/details/118120055
一、概述
JavaScript内部,所有数字都是以64位浮点数形式存储,即使整数也是如此。所以,1和1.0是相同的,是同一个数。
1 === 1.0 // true二、理论上:浮点数
双精度浮点数占用8字节的存储空间,64bit位,一个符号位,11位指数位,52位小数部分。
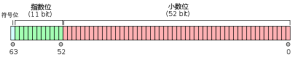
一般我们都知道js能表示的最大数值是1.7976931348623157e+308,那么这个值具体怎么得出的呢?
先看看浮点数值的计算方法,类似于10进制的科学计数法
公式:value = (-1)^符号位 * 小数位 * 2^指数位
1、符号位:
仅有一位,0为正数,1为负数
公式(正数):value = (-1)^0 * 小数位 * 2^指数位
公式(负数):value = (-1)^1 * 小数位 * 2^指数位
2、指数位:
指数位有11位,取值范围就是[0, 2^11 – 1] = [0, 2047],如果指数位取值都是正数,那么我们只能表示大于1的数字,无法表示小数了。于是我们规定一个偏移量1023,指数的取值范围变成[-1023, 1024]。不考虑指数=0和2047的情况,指数的取值范围是 [-1022, 1023]
公式:value = (-1)^0 * 小数位 * 2^1023 (最大值为例)
3、小数位:
小数位有52位,这个地方有个隐藏的1,大家知道科学计数法都是大于1的数字,举个栗子:1.254E3, 1.254总是大于1,也就是小数点前一位一定是1,那我们就把他设为默认的,无需占用64位中的一位了。那么小数位的范围是[0, 1 – 2^(-52)] 。这个是怎么计算的呢?52位有点长,看下普通的二进制:0.111 转为10进制,结果是(2^3 – 1) / 2^3 = 1 – 2^(-3) = 0.875,那么52位的也就是[0, 1 – 2^(-52)]。因为我们小数点前还有个1,所以这块取值范围是[1, 2-2^-52]
公式:value = (-1)^0 * [2-2^(-52)] * 2^1023 (最大值为例)
那我们计算下最大值:
2-2^(-52) ≈ 2
value ≈ 2 * 2^1023 = 2^1024 = 1.7976931348623157e+308
三、实际上:整数
小数点前面的1,加上52位小数位,共计53个bit位表示整数,指数位为0,那么最大整数为:
±2^53 = 9007199254740992